Operaciones Básicas MATHEMATICA
1.- Obtener la integral 
Cuando se multiplican dos variables, se debe dejar un espacio entre ellas, o bién, utilizar el paréntesis. El argumento de la función trigonométrica o logarítmica debe de estar entre corchetes.
La integral se resuelve con la instrucción:
Integrate[x Cos[2x],x]
Siendo el resultado: 
2.- Obtener la integral 
La instrucción que se aplica es:
(el símbolo de la constante e se escribe como E, como es el produto de dos funciones se debe dejar un espacio entre ellas)
Integrate[E^(-2x) Sin[3x],x]
El resultado es: 
3.- La integral 
(el símbolo del logaritmo natural Ln se escribe como Log, se deja un espacio entre las dos funciones)
La instrucción es: Integrate[y Log[2y],y]
Siendo el resultado: 
4.- Derivar la expresión 
La instrucción es: D[E^(3x) Tan[2x],x]
El resultado es: 
5.- Obtener el límite 
La instrucción es: Limit[(x^2-3x+10)/(x-5), x->2]
El resultado es: 
6.- Obtener el límite 
La instrucción es: Limit[E^x/x , x->Infinity]
Siendo el resultado: 
7.- Realizar la operación 
Instrucción: Expand[(x+2)^3 ]
El resultado es: 
8.- Factorizar: 
La instrucción es: Factor[x^3+6x^2+12x+8]
Siendo el resultado: 
Para pedir que nos exprese la función Sen3t como función imaginaria:
La instrucción es: TrigToExp[Sin[3t]]
El resultado es: 
La función Cos3t en función imaginaria: TrigToExp[Cos[3t]]
El resultado es: 
; siendo 
Para una identidad trigonométrica: TrigExpand[Cos[2x]]
El resultado es: 
Si deseamos obtener una identidad trigonométrica más simple:
(dejar un espacio entre las funciones)
TrigReduce[Cos[a] Cos[b]-Sin[a] Sin[b]
El resultado es: Cos[a+b]
Práctica Número 1
Ecuaciones Algebraicas de Variables Separables
Objetivo:
Que el alumno obtenga la solución general de dos ecuaciones diferenciales de variables separables, y utilizando el Mathematica compruebe los resultados, grafique las soluciones, y posteriormente las interprete.
Procedimiento:
Lee cuidadosamente los ejemplos resueltos en el Mathematica, posteriormente selecciona y resuelve dos de las ecuaciones que se presentan al final. Cuando las hayas resuelto, con el Mathematica comprueba los resultados y grafica la solución. Posterirmente interpreta la gráfica de la solución.
Antecedentes:
Ejemplo 1) La ecuación 
para resolverla en el Mathematica, deben separarse las variables con su correspondiente diferencial, luego integrar ambos términos por separado:
Integrando el lado izquierdo: Integrate[(2x^3+x^2+3)/x , x]
Siendo el resultado: 
Integrando el lado derecho:Integrate[(y^2+2)/y , y]
El resultado es: 
El resultado final es la igualdad de los dos resultados, agregando a constante C de integración:
Para obtener la gráfica, como no se pues de depejar la x o la y , es necesario expresar entonces a la constante C como una función de x y de y: C(x,y). El resultado de la gráfica se obtiene con la instrucción:
ContourPlot[2x^3/3+3Log[x]+x^2/2-y^2/2-2Log[y],{x,0.1,3},{y,0.1,1},ContourShading->False]
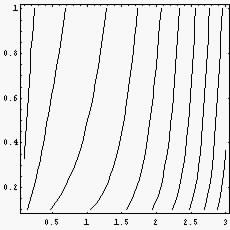
Ejempo 2) La ecuación de variables separables 
se resuelve separando las variables con su correspondiente diferencial, posteriormente
se integran ambos términos por separado:
Integrando el lado izquierdo: Integrate[(x^2+2)/(x(x+1)) ,x]
Siendo el resultado: 
Integrando el lado derecho: Integrate[Tan[y] , y]
Siendo el resultado: -Log [Cos[y]]
La solución general es la igualdad de ambos resultados, agregando la constante C de integración:
(Log significa logaritmo natural: Ln )
Ejemplo 3) Resolver la ecuación de variables separables con las condiciones que se indican:
Como es una ecuación con condiciones iniciales, el procedimiento de solución es diferente, primero se resolverá aplicando la condición de que en t=0, T=70:
idicando que T es función de t : Dsolve[{ T ‘[t]==k(T [t] – 20),T[0] == 70}, T[t], t ]
Siendo la respuesta: 
Luego se pide que obtenga el valor de la constante k, con la condición de que en t=5,
T=30. Instrucción: NSolve[30==20+50E^(5k), k]
Siendo la respuesta: k= – 0.032188
Se pide que se reemplace el valor de la constante K en la solución general obtenida en el paso 4, en este caso, del Mathematica:
Replace[%4 /. K-> – 0.032188]
Siendo la respuesta: 
Por lo que la solución particular es: 
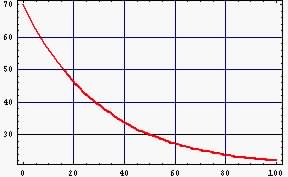
Su gráfica correspondiente:
Plot[20+50E^(-0.032188 t), {t,0,100},Frame->True,GridLines->Automatic,
PlotStyle->{RGBColor[1,0,0],Thickness[0.01]}]
Ecuaciones Selectivas:
Selecciona dos ecuaciones de las que se presentan a continuación, resolverlas, y con el Mathematica comprobar la solución y graficarla. Interpreta las gráficas solución:
1) 
2) 
3) 
4) 
5) 
condiciones: t=0,T=20; t=3,T=30
6) 
7) 
8) 